La estadística es de 1 en 2000 que le caigan a solamente una de las 7 mil millones de personas. No las chances de cada persona de que le caigan.
Lo que es totalmente diferente.
Sigue siendo amplísimamente mayor las chances que te ganes la lotería.
Estadística del periodismo
Hay 7.000.000.000 personas en el mundo
La probabilidad de que caiga sobre una persona un cachito de satélite, según los diarios: 1 en 2000
Unas 3.500.000 personas recibirán su dosis de cascotazo de satélite según los medios entre el 20 y 25 de este mes.
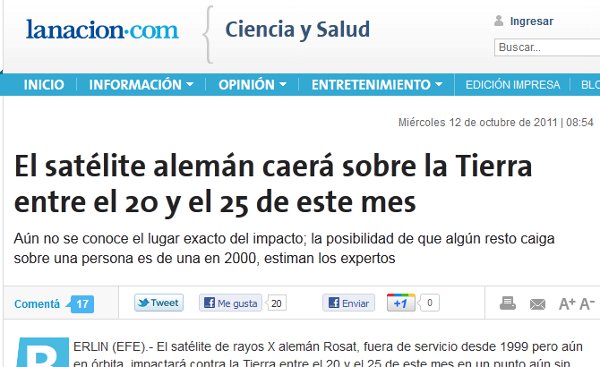
Ya con el satélite anterior habían dicho la misma pelotudez, hoy le tocó a La Nación copypastear mal
En un planeta con un 75% de Océanos, con el planeta tan poco densamente poblado como está (la distribución es horrible, lleno de áreas sin población), si la probabilidad de que pegue en alguien es de 1 en 2000, prepárense, que el planeta se llenará de cascotazos, hasta diría que aumentará su masa
Tip: la próxima vez digan "1 en 2000 en un área de x kilómetros cuadrados" y ahí la cosa cambia TOTALMENTE , pero deberían analizar el área y combinarla con la densidad poblacional, ahí hagan las cuentas y vemos
Otros posts que podrían llegar a gustarte...
Comentarios
-
Así como yo lo entiendo se refiere a que la probabilidad es de 1 en 2000 de que le caiga a alguna persona cualquiera. La probabilidad de que le caiga a alguien en concreto es muuuuuuuuuuuuuuuuucho mas pequeña.
-
Guille dijo:
La estadística es de 1 en 2000 que le caigan a solamente una de las 7 mil millones de personas. No las chances de cada persona de que le caigan.
Lo que es totalmente diferente.
Sigue siendo amplísimamente mayor las chances que te ganes la lotería.
no, justamente es lo mismo, si hay 1/2000 de que le pegue a cualquier persona hablás entonces de los 7.000 millones mundiales, en cambio si es 1/2000 * 7.000.000.000
la cifra es tan ínfimamente baja que se torna irrelevante, en cambio poniendo 1/2000 da más miedito mediático
-
Guille dijo:
La estadística es de 1 en 2000 que le caigan a solamente una de las 7 mil millones de personas. No las chances de cada persona de que le caigan.
Lo que es totalmente diferente.
Sigue siendo amplísimamente mayor las chances que te ganes la lotería.
Estoy de acuerdo con Gille, es la probabilidad de que le caiga a alguna de esas 7.000.000.000 de personas, no la de cada uno...
-
Fabio dijo:
Guille dijo:
La estadística es de 1 en 2000 que le caigan a solamente una de las 7 mil millones de personas. No las chances de cada persona de que le caigan.
Lo que es totalmente diferente.
Sigue siendo amplísimamente mayor las chances que te ganes la lotería.
no, justamente es lo mismo, si hay 1/2000 de que le pegue a cualquier persona hablás entonces de los 7.000 millones mundiales, en cambio si es 1/2000 * 7.000.000.000
la cifra es tan ínfimamente baja que se torna irrelevante, en cambio poniendo 1/2000 da más miedito mediático
Creo que no entendés a qué va el comentario. Siendo que tengo un espacio vacío del 90% y un espacio ocupado con personas de un 10%, hay un 10% de probabilidades de que, al revolear un satélite, le pegue a alguien cualquiera. La probabilidad ahí sería de una en 10.
Al mismo tiempo, siendo que la Tierra tiene un espacio ocupado por personas de 1/2000 (no sé si la cifra será ésa, pero asumamos que sí) tendrían razón.
-
No salio la imagen Fabio
poco opulation_density.png">densamente poblado como está
Buen post, como siempre.
Salu´´
-
Coincido con los que ya comentaron, ya extrapolación que hacés no tiene sentido.
A ver, imaginate un tablero cuadriculado, tipo buscaminas, de 100x100 casilleros. El tablero tiene 10.000 casilleros. Supongamos que distribuyo de cualquier forma 1.000 personas entre esos casilleros. Ahora, imaginate que en un casillero al azar detona una mina que solo lastimaría a alguien que esté en ese casillero.
¿Cuál es la probabilidad de lastimar a una persona? Bueno, si tengo 1.000 personas distribuidas en 10.000 casilleros. La probabilidad de que haya una persona en un casillero cualquiera es 1.000/10.000 = 10% o 1 en 10.
Ahora bien, si hiciéramos el razonamiento del post en el ejemplo, multiplicaríamos 1 en 10 (10%) por 1.000 personas y diríamos que 100 personas serán voladas por una mina, lo cual obviamente no es cierto porque dijimos que solo una mina va a estallar.
Finalmente, como bien dijo Santiago, 1 en 2000 es la probabilidad de que le pegue a una persona cualquiera de los 7 mil millones, no la probabilidad que tiene cada persona de ser impactada. En mi ejemplo, la probabilidad de que le estalle la mina a una persona cualquiera es 10% pero la probabilidad que tiene cada persona de ser impactada es de 1 en 10.000, como ves, muchísimo menor.
-
Cabe resaltar que, si bien no se sabe la ubicación exacta de la caída, deben ya tener un margen (no es que el satélite se mueve de manera totalmente errática por toda la tierra) por lo cual, además de lo dicho anteriormente, la cantidad de personas no está ni cerca de 7 000 000 000.
Sí, un dato que no aporta un carajo, teniendo en cuenta lo que se dijo antes, pero yo de troll nada más.
Edit: Efectivamente...
los expertos tan sólo pueden precisar que el Rosat caerá sobre la Tierra entre el 20 y el 25 de octubre, con un margen de error de más o menos tres días, y entre los 53 grados de latitud norte y los 53 grados de latitud sur
-
Las matemáticas y el periodismo no se llevan bien... hace años un periodista de La Nación intentó calcular el volumen físico de cierta cantidad de dinero, robado) llegando a la conclusión que eran como 3m³ algo que cabía en una valija...
son de terror y lo exponen sin problemas.
-
Parece que hay unanimidad en que Fabio entendió mal. Vine solmamente a decir lo mismo que dijeron todos

-
Yo leí la nota en el diario y pensé lo mismo. Una probabilidad de 1/2000 es altísima, yo por las dudas ese día no salgo...

-
Claramente es una cuestión de que interpretaste mal la estadística. Lo que dice es que la probabilidad de que le pegue a alguien en alguna parte del planeta es de 1/2000. Es decir, de otra manera, si cayeran 2000 satélites idénticos es muy probable que le pegaran a alguien.
Como justamente decís que hay 7.000.000.000 personas, la probabilidad de que le caiga a alguien en particular es de 1/14e12.
-
me sumo a la lista de quienes piensan que fabio entendió mal.
dice "una persona" en el sentido de cantidad (igual a 1), no en el de pedro, juan, o quien sea .quizás da para confusión , pero ciertamente no es incorrecto.
-
GoFa dijo:
Edit: Efectivamente...
los expertos tan sólo pueden precisar que el Rosat caerá sobre la Tierra entre el 20 y el 25 de octubre, con un margen de error de más o menos tres días, y entre los 53 grados de latitud norte y los 53 grados de latitud
sur
digamos que es una precision apestosa esa! el ´rango de la orbita´ va mas o menos de 53n a 53s y en 5 dias da mas de 15 vueltas
aca se puede trackear: http://www.n2yo.com/?s=20638
-
Déjense de joder... ya cayó el satélite de la NASA, hicieron un quilombo bárbaro y no le dio a nadie, hasta insinuaron que le había dado a una casa en el conurbano.
Ahora, si vamos a tener todos los meses un satélite cayendo sin control es para preocuparse...
¿Cuántos satélites hay en órbita? ¿Puede ser que haya leído que hay cerca de 2500?
-
Básicamente la estadística dice que tenés que tener muuuuuuucha mala leche para que te caiga encima.
-
¿Y el efecto esquive? ¿Dónde m... lo meten en los cálculos?
¿O creen que si alguien ve venir un bólido en su dirección se va a quedar inmóvil esperando que le pegue?
-
Como dijeron por ahi, cualquier estudiante de estadística, sacaría la población en el área que cubre el satélite y (suponiendo que esta uniformemente distribuida en esa region, lo cual ya es una locura total), hay que usar el área de peligro, el área que ocupa una persona, el área de las piezas que caen, la cantidad de las mismas y entonces la probabilidad sale de hacer la cuenta con esos elementos. Todo eso suponiendo que el satelite esparce sus piezas uniformemente en el área, lo cual no es cierto y habría que hacer una simulación. Cualquier otra cosa es una mentira. Es increible como algo como un diario que influye sobre las opinion general, saque algo asi. Yo me la paso inculcando que NO lean articulos de ciencia de los diarios, la gran mayoría comente errores que ni un aficionado a la ciencia cometería. Han dicho mentiras terribles que son fáciles de comprobar y la gente sigue comprando diarios y creyendo. Digo yo, tanto cuesta pedir disculpas si se equivocaron?, si no lo hacen es porque no les interesa nada mas que vender a toda costa. A propósito de esto, hace un tiempo en un estudio en el que se analizó la erosion costera en un lugar específico de la costa atántica, se publicó un paper con los valores medios de la erosion en la costa en esa zona y el diario del instrumento musical publico un titular que decia que el mar habia avanzado 30 metros, sin especificar el tiempo en el cual habia pasado eso ni el área. O sea, la intención es vender como sea, sin importar lo que dicen, sin tener la mas mínima conciencia como integrantes de una sociedad, sin importar involucrar a otras personas en el proceso de ganar plata.
-
de todos los que me dijeron que mi cálculo estaba mal: están mal y explico por qué: estan fijándose en lo que uds. con su inteligencia, interpretan y no en el mensaje confuso del artículo de LNOL que es el quid de la cuestión.
si la probabilidad de que a alguno de los 7.000 millones de habitantes de la tierra le pegue un cachito de satélite es de 1/2000, es que a vos, yo, o cualquiera de los 7MM les de en el marote "algo" del satélite.
me lo dicen y repiten una y otra vez, okey, 1/2000 ES UNA BARBARIDAD DE ALTO por individuo pero ahí está el truco.
Si la proporción fuese correcta debería ser 1/2000 distribuído en 7MM, da 3.5 millones, pero s200i fuese la que deberían calcular es 1/(2000 * 7.000.000.000) y esa es la probabilidad correcta de que le de a cualquiera de ustedes.
Tan sólo mirar tantos ceros complica pero 1/14.000.000.000.000 es más coherente que 1/2000 y es la cifra que se debería haber publicado.
Y no, la probabilidad jamás la podés proponer como "hay una 1/2000 chances de que al menos a alguno le pegue, cosa que la nota no facilita y es la interpretación que le damos por lógica.
Pero usar el dato de fracción para no dar el número real, ESO ES LO PEOR! el número real es 1/14.000.000.000.000, por ende, con ese número, no tendrías nota.
Considerando la posición donde se estima que caerá, una locación con menos de un habitante por kilómetro cuadrado, hasta el número 1/2000 es erróneo en el área afectada.
El único fin es generar interés, miedo de doña rosa y una nota leída, no informar.
-
Sí Fabio, estoy de acuerdo con los comentarios, entendiste mal esta vez.
Dijiste justamente lo que alguien sin conocimientos de probabilidad interpretaría:
"Unas 3.500.000 personas recibirán su dosis de cascotazo de satélite según los medios entre el 20 y 25 de este mes. "
-
Estamos en condiciones de afirmar que es mas probable que te caiga un satelite en la cabeza a que Fabio de el brazo a torcer?
-
Coincido plenamente con los comentarios. Cuando leí la nota, creo quedó claro.
Por otro lado, estás subestimando la capacidad del lector de La Nación, donde no son todos "Doñas Rosas".
Saludos.
-
Los únicos diarios Argentinos ( ¿o pasquines? ) que manejan bien las cifras son Ambito Financiero y El Cronista, a los demás los ceros los omnubilan.
-
Fabio dijo:
de todos los que me dijeron que mi cálculo estaba mal: están mal y explico por qué: estan fijándose en lo que uds. con su inteligencia, interpretan y no en el mensaje confuso del artículo de LNOL que es el quid de la cuestión.
si la probabilidad de que a alguno de los 7.000 millones de habitantes de la tierra le pegue un cachito de satélite es de 1/2000, es que a vos, yo, o cualquiera de los 7MM les de en el marote "algo" del satélite.
me lo dicen y repiten una y otra vez, okey, 1/2000 ES UNA BARBARIDAD DE ALTO por individuo pero ahí está el truco.
Si la proporción fuese correcta debería ser 1/2000 distribuído en 7MM, da 3.5 millones, pero s200i fuese la que deberían calcular es 1/(2000 * 7.000.000.000) y esa es la probabilidad correcta de que le de a cualquiera de ustedes.
Tan sólo mirar tantos ceros complica pero 1/14.000.000.000.000 es más coherente que 1/2000 y es la cifra que se debería haber publicado.
Y no, la probabilidad jamás la podés proponer como "hay una 1/2000 chances de que al menos a alguno le pegue, cosa que la nota no facilita y es la interpretación que le damos por lógica.
Pero usar el dato de fracción para no dar el número real, ESO ES LO PEOR! el número real es 1/14.000.000.000.000, por ende, con ese número, no tendrías nota.
Considerando la posición donde se estima que caerá, una locación con menos de un habitante por kilómetro cuadrado, hasta el número 1/2000 es erróneo en el área afectada.
El único fin es generar interés, miedo de doña rosa y una nota leída, no informar.
Yo sigo creyendo que estás equivocado.
No veo porqué se tomaría en cuenta el número de personas para disminuir la probabilidad. ¡Todo lo contrario! Mientras más personas haya la probabilidad debería aumentar.
Supongamos que el planeta estuviera 100% ocupado por personas. Las probabilidades de que el satélite golpeara a alguien serían del 100%, sería ridículo pensar que la probabilidad disminuya habiendo más personas.
Es decir, dado el caso de que con 10 000 000 000 000 (número tirado al voleo ) ocupáramos TODA la Tierra, la probabilidad de que el satélite golpée a una persona ni en pedo sería de 1 / 10 000 000 000 000.
) ocupáramos TODA la Tierra, la probabilidad de que el satélite golpée a una persona ni en pedo sería de 1 / 10 000 000 000 000.
-
nacho dijo:
GoFa dijo:
Edit: Efectivamente...
los expertos tan sólo pueden precisar que el Rosat caerá sobre la Tierra entre el 20 y el 25 de octubre, con un margen de error de más o menos tres días, y entre los 53 grados de latitud norte y los 53 grados de latitud
sur
digamos que es una precision apestosa esa! el ´rango de la orbita´ va mas o menos de 53n a 53s y en 5 dias da mas de 15 vueltas
aca se puede trackear: http://www.n2yo.com/?s=20638
Claro, pero eso excluye a países del norte de europa, Canadá, parte de Rusia, etc. en la ecuación.
-
Fabio, estás interpretando al revés lo que dice la oración
NO ES 1/2000 de que una persona reciba un escombro
ES 1/2000 de que un escombro pegue en una persona
El 1 no es una persona x, sino un escombro x.